ahp层次分析法博文__ahp群决策矩阵
1. 如何显示群决策矩阵
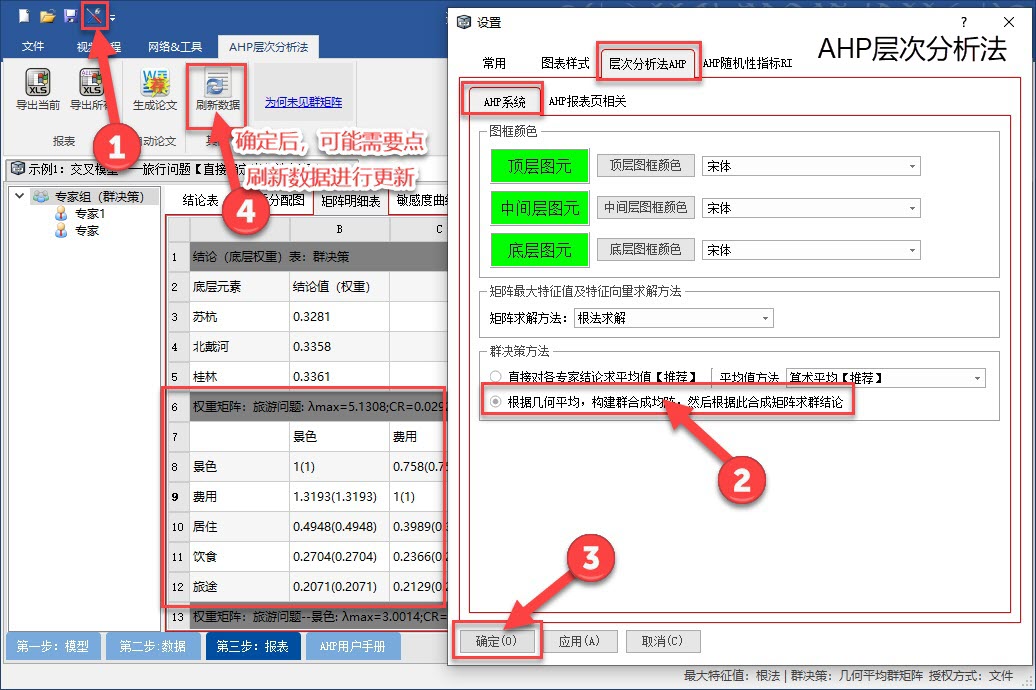
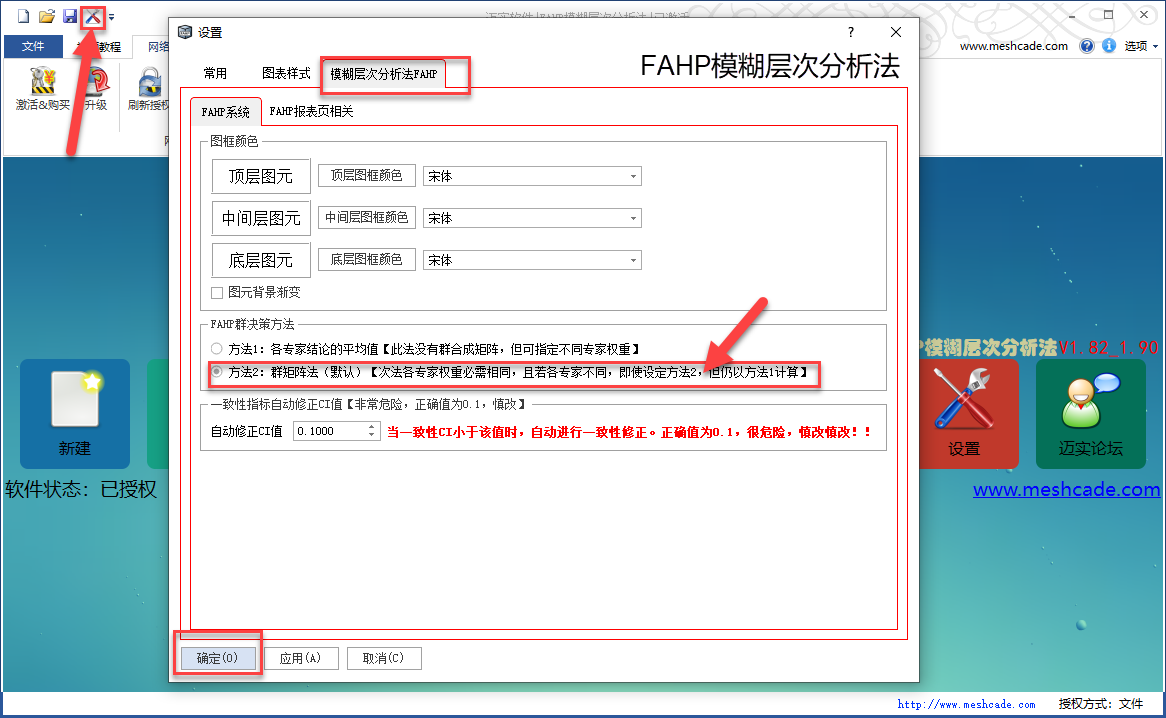
特别说明： 若各专家的权重值不同,由于无法获得几何平均值,相应也就无法求得群矩阵，此时软件还是以算数平均法计算群结论。【即此时即使设置了群矩阵法，仍然无法获得群矩阵】
若需深入了解原理，可继续向下阅读，反之可忽略下文
2. 如何求得的AHP群决策矩阵
2.1 假如AHP专家1（Z1）的某打分矩阵为
| A | B | |
| A | 1 | 2 |
| B | 1/2 | 1 |
2.2 假如AHP专家2（Z2）的某打分矩阵为
| A | B | |
| A | 1 | 4 |
| B | 1/4 | 1 |
2.3 正确获得AHP群决策矩阵(几何平均，正确)
| A | B | |
| A | （1*1)^0.5 | （2*4）^0.5 |
| B | （1/2*1/4)^0.5 | (1*1)^0.5 |
即
| A | B | |
| A | 1 | 2.8284 |
| B | 1/2.8284 | 1 |
2.4 错误获得AHP群决策矩阵(算数平均，错误！！！)
| A | B | |
| A | （1+1)/2 | （2+4）/2 |
| B | （1/2+1/4)/2 | (1+1)/2 |
即
| A | B | |
| A | 1 | 3 |
| B | 3/8 | 1 |
解释：此错误是由于当第一行 A:B = 3时，第二行B:A应等于1/3；或者 第二行B:A应等于3/8时，第一行A:B应等于8/3。 故算数平均的合成矩阵是错误的！！！
再次强调，本2.4条算数平均求AHP群矩阵为错误的算法，以2.3为准！！！
3. 如何求得的FAHP群决策矩阵
3.1 假如FAHP专家1（Z1）的某打分矩阵为
| A | B | |
| A | 0.5 | 0.9 |
| B | 0.1 | 0.5 |
3.2 假如FAHP专家2（Z2）的某打分矩阵为
| A | B | |
| A | 0.5 | 0.7 |
| B | 0.3 | 0.5 |
3.3 获得FAHP群决策矩阵
| A | B | |
| A | （0.5+0.5)/2 | （0.9+0.7）/2 |
| B | （0.1+0.3)/2 | (0.5+0.5)/2 |
即
| A | B | |
| A | 0.5 | 0.8 |
| B | 0.2 | 0.5 |
说明，与AHP不同，FAHP可直接通过求矩阵的算数平均即可获得群矩阵。
4.若不通过群矩阵，如何得到的群结论【推荐此方法】
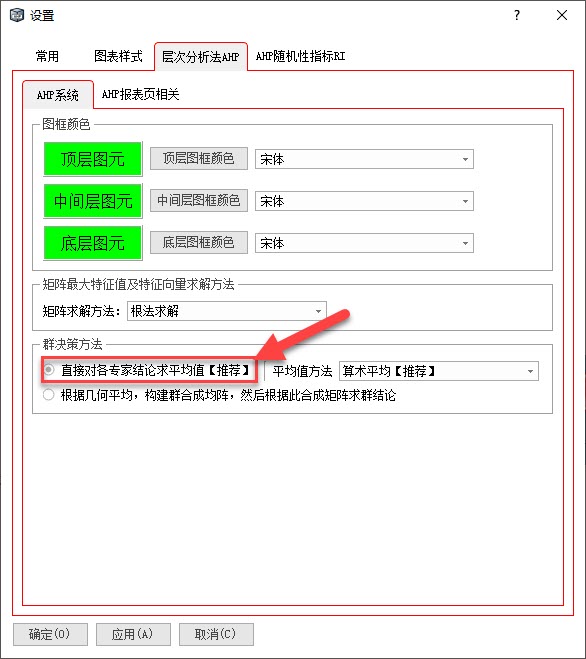
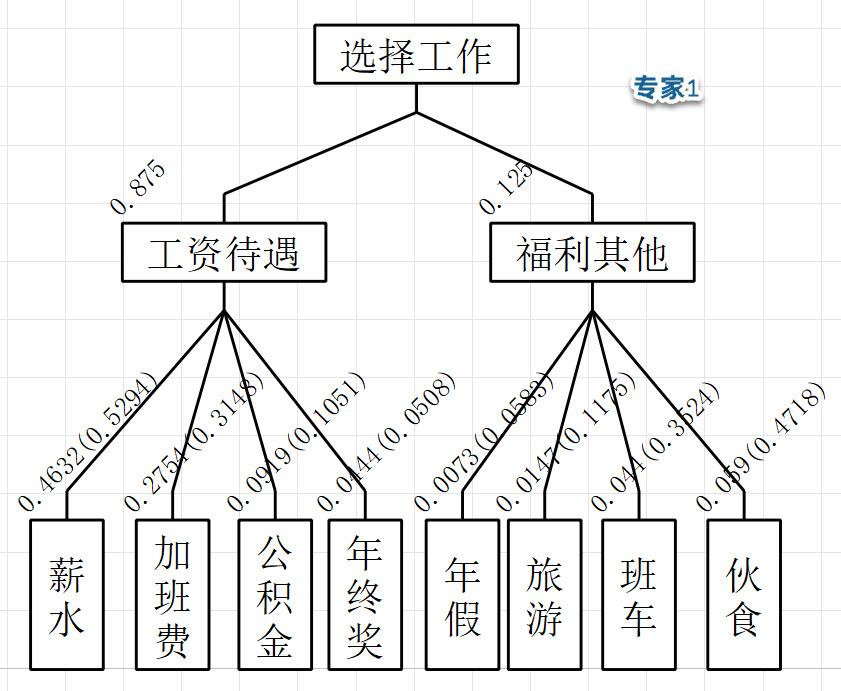
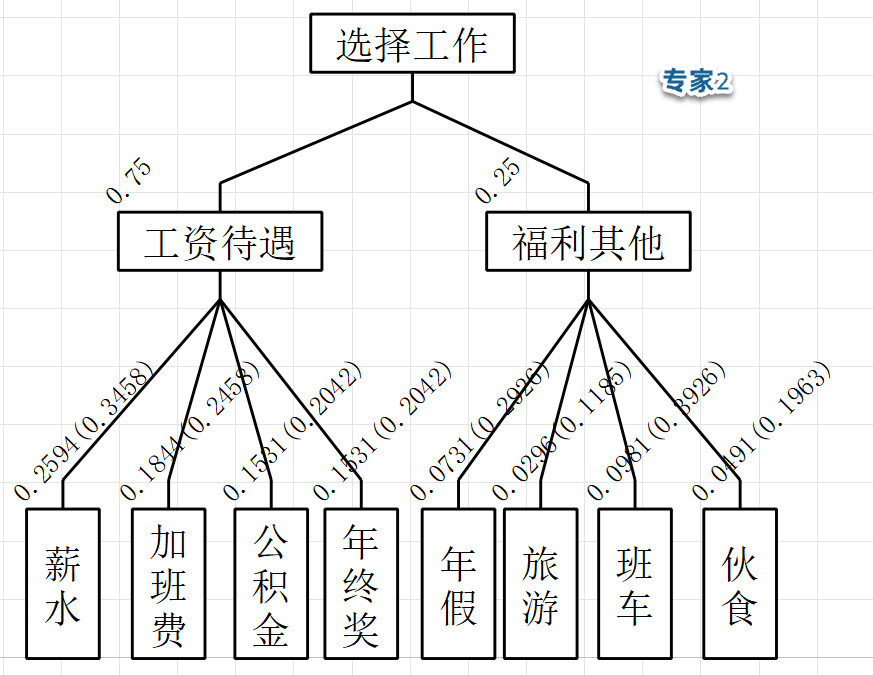
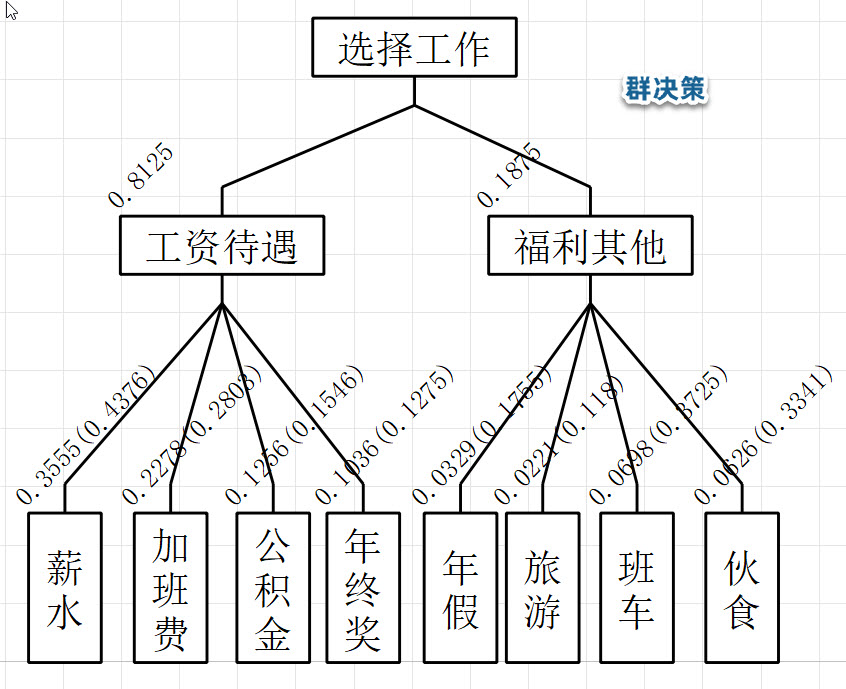
则薪水的平均同级权重S1=(0.5294+0.3458)/2=0.4376，工资待遇的平均权重S2=(0.875+0.75)/2=0.8125,则薪水的最终群权重S3=S2xS1=0.8125x0.4376=0.3555。其余指标类似
常见的错误算法：是薪水最终权重S3=(0.4632+0.2594)/2=0.3613，但此时很明显无法保证S3等于S2xS1
相关知识：交叉模型如何算出的底层结论呀？
5.什么是同级权重和全局权重
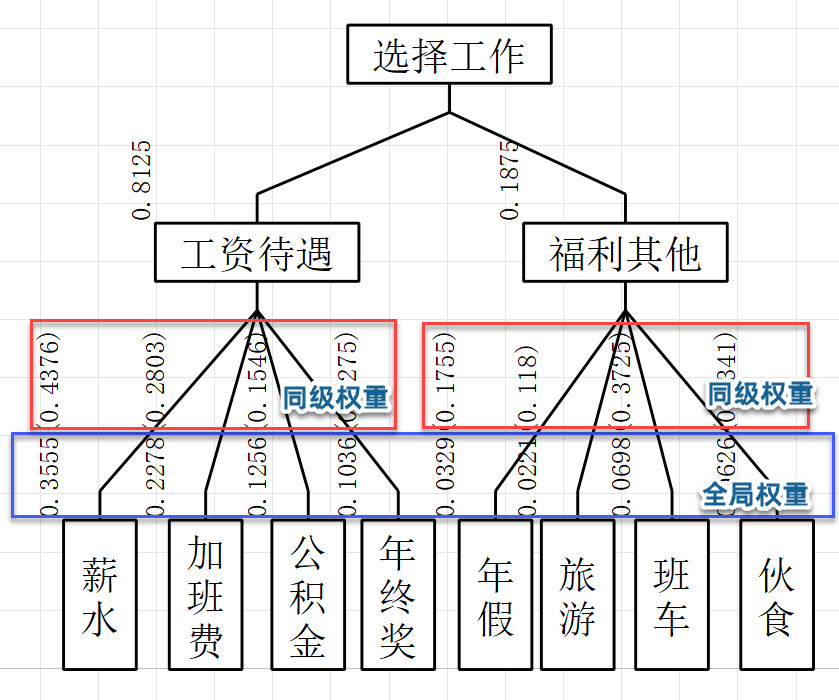● 同级权重表示同一父节点下的对比权重（亲兄弟权重），各同级权重相加=1；
● 全局权重表示同级所有节点的对比权重（表兄弟权重），所有全局权重相加=1；
● 使用时主要用全局权重
6.群决策矩阵的补充说明
● 若各专家的权重值不同,由于无法获得几何平均值,相应也就无法求得群矩阵，此时软件也将会自动还以算数平均法计算群结论。【即此时即使设置了群矩阵法，仍然无法获得群矩阵】
● 群决策的群决策矩阵法与算数平均法的结论（即结果值）通常会有所不同。
● 建议是以算数平均法求群结论，而非群决策矩阵法。
●通过前文的推导步骤可知，由于群矩阵是通过几何平均数获得的，故很难是整数（整分数），故若某论文中的群矩阵全是整（分）数，则其准确性值得商榷。